레너드 오일러 - 수학의 천재 그리고 성경을 믿는 기독교인 - Russell Grigg 글, 이종헌 역

레너드 오일러

수학의 천재 그리고 성경을 믿는 기독교인

 

Russell Grigg 글, 이종헌 역

출처: creation magazine Vol. 40(2018), No. 4 pp. 48-52

 

 

 

 

 

* 이 기사는 저자의 훨씬 더 광범위하고 보다 더 문서화된 동일 이름의 기사인 creation.com/euler를 압축한 것이다.

 

레너드 오일러(LEONHARD EULER)(1707-1783)는 모든 시대에 걸쳐 가장 위대한 수학자이자 이론 물리학자 중 한 명이었으며, 또한 가장 다작을 했다. 그는 순수 수학과 응용 수학의 거의 모든 영역, 특히 미적분학, 수론, 표기법, 광학 및 천체, 유리수 및 유체 역학에 기여했다.(1)

 

그는 물리 문제에 수학을 적용함으로써 지도제작, 연대학, 선박 건조, 교량 건설 및 탄도학에 많은 실질적인 발전을 이루었다. 이러한 여러 업적은 그로 하여금 아르키메데스, 뉴턴 및 가우스의 반열에 오르게 했다. 저명한 스위스의 과학 역사학자 에밀 펠만(Eminer Fellmann)은 오일러가 “모든 인류 역사에서 지금까지 가장 생산적인 수학자 일뿐만 아니라 모든 시대에 걸쳐 가장 위대한 학자 중 하나”라고 말했다.(2)

 

 

Early life and a talent for mathematics(초기의 삶과 수학에 대한 재능)

 

레너드(Leonhard)는 1707 년 스위스 바젤에서 태어났다. 수학을 공부 한 그의 아버지는 “기독교인의 내면의 중생의 삶, 형제애, 그리고 살아있는 믿음”을 강조한 복음주의 개혁 교회의 목사였다.(3) 이것들은 레너드 자신이 받아들인 신념이었고 이로 인해 그는 결코 흔들리지 않았다.

 

젊은 레너드는 집에서 아버지에게 수학의 원리를 소개받았다. 그는 1720년에 목사가 되기 위해 바젤대학(University of Basel)에 등록했다. 거기서 가족의 친구이며 나중에 유럽에서 가장 유명한 수학자 중 한 명이 된 요한 베르누이(Johann Bernoulli)에게서 수학을 배웠다. 베르누이는 레너드가 이 과목에 대한 특별한 재능과 열심을 가지고 있는 것에 감명을 받아서 레너드에게 토요일 오후에 개인적으로 수학, 천문학 및 물리학을 교습했을 뿐만 아니라, 그의 아버지에게 이 아들이 신학이 아니라 수학 쪽에서의 직업을 타고났다고 확신시켰다.

 

 

Entering the  Paris Prize competition(파리 상 대회에 참가하다)

 

1727년에 오일러(Euler)는 당시에 유럽에서 가장 뛰어난 과학상인 파리 과학 아카데미(Paris Academy of Science)의 파리 상 경연에 논문을 제출했다. 그의 에세이는 항해하는 배가 최대 속도를 달성하기 위해 돛대를 배치하는(돛의 수, 위치 및 높이) 가장 좋은 방법에 관한 것이었으며, 등외 가작 표창을 받았다. 그 후 몇 년 동안 그는 두 번 더 등외 가작 표창을 받았으며, 그가 참가신청을 한 12 차례의 다른 기회에서 상을 받거나 공동 수상을 했다.

 

 

Time in Russia(러시아에서의 시기)

 

1727년에서 1741년까지, 오일러는 쌍트 페텔스부르크(St Petersburg)에 있는 제국 과학 아카데미(Imperial Academy of Science)에서 가르쳤으며, 거기서 그는 1731년에 물리학 교수가 되었고, 2년 후 수학과의 학과장으로 임명되었다. 그의 전기 작가인 Ronald Calinger는 그의 연구가 “대수학, 산수, 천문학, 탄도학, 원뿔형 단면, 미분 기하학, 탄성학, 무한 급수, 음악 이론, 수 이론 및 진동” 등을 광범위하게 다루었으며 그의 주요 분야는 이론 역학이었다. 수리 과학의 통합을 확신한 오일러는 각각의 분야를 완성하는 것에 착수했다.“라고 쓰고 있다.(4)

 

그는 소방차 설계, 러시아 해군 자문, 러시아 학교 교과서 저술, 뿐만 아니라 독일어 초급 산수 2 권 등 실용적인 활동에도 참여했습니다. 그는 또한 러시아 제국 전체의 첫 번째 정확한 대규모지도를 준비하는 데 도움을 주었다. 그것은 1745년에 러시아 지도책(Russian Atlas)으로 발표되었는데, 거기에는 경도와 위도를 정확하게 결정하는 것이 필요했다.

 

 

Marriage and family(결혼과 가족)

 

1734 년에 오일러는 카타리나 그셀(Katharina Gsell)과 결혼했으며, 13명의 자녀를 두었다. 슬프게도 그 중 5 명만이 어린 시절 생존했으며, 3명만이 부모보다 오래 살았다. 칼린저는 이렇게 적고 있다:

 

매일 저녁 식사 후 저녁마다 오일러는 자기 자녀들과 하인들과 그의 집에서 하숙하는 학생들을 불러 모아서 가정 예배를 드렸다. 거기서 성경을 읽고 때로는 설명과 토론을 하였다. 잠자리에 들기 전에 그는 종종 자기 자녀들에게 성경 구절이나 성경 이야기를 읽어주었다.(5)

 

 

Solving the Basel problem(바젤 문제를 해결하다)

 

1735 년에 오일러는 1644 년에 처음 문제가 제기된 이래로 세계 최고의 수학자들을 당혹스럽게 만든 수치 퍼즐을 풀어서 즉각적으로 명성을 얻었다. 그것은 자연수의 제곱의 역수에 대한 정확한 합을 증명과 함께 요구하는 것이다. 즉, 다음 무한급수의 정확한 합:

 

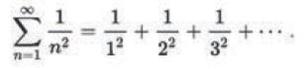
오일러는 n이 무한대로 접근할 때 이 급수의 합이 π2/6임을 증명했다. ‘수학적인 소양이 있는’ 독자들은 영어로 된 그의 증명을 wikipedia.org/wiki/Basel_problem에서 볼 수 있다.

 

 

Resolving the ‘Seven Bridges of Konigsberg’ problem

(‘Konigsberg의 일곱 개의 교량’ 문제를 해결하다)

 

동 프로이센에 있는 오래 된 도시 쾨니히스베르그(Königsberg)(현재 러시아의 칼리닌그라드)는 이전에 네 개의 땅덩어리를 가지고 있었는데, 이들은 아래의 도표에 나타난 바와 같이 프레겔 강(Pregel River)을 가로 지르는 7개의 교량으로 연결되어 있었다.

 

 

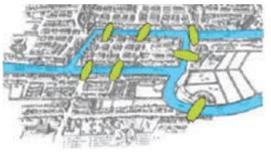
(그림 3) 오일러 시대의 쾨니히스베르크의 지도

 

 

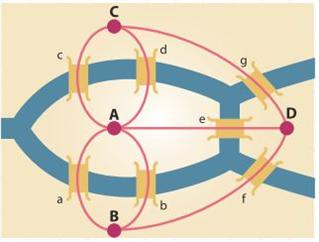
(그림 4) 쾨니히스베르크 문제에 관한 현대의 기하학적 표현

 

시민들은 한번의 산책에서 각 다리를 한 번씩만 건너며 이들 네 개의 지역을 모두 가 보는 것을 시도하며 그들의 여가 시간을 보냈다.

 

아무도 그것을 하지 못했지만, 아무도 그것을 할 수 없다고 단호하게 말할 수는 없었던 것 같다. 오일러가 들어왔다! 1735년에 그는 논리의 거대한 도움과 약간의 산수를 이용하여 이 문제를 해결했다. 그는 다음과 같이 지적했다:

 

* 각 지역 내의 경로 선택은 서로 무관하다.

* 각 지역을 들어오고 나가는 데에는 두 개의 서로 다른 교량을 사용해야만 한다.

* 따라서 각 지역은 짝수 개의 다리가 있어야 한다.

* 그러나, 한 지역에는 다섯 개의 다리가 있으며 세 개의 지역에는 각각 세 개의 다리가 있다.

* 그러므로 지정된 대로 걷기가 불가능하다.

 

오일러의 해는 현대 그래프 이론의 토대를 마련했고 위상학의 개념을 예시했다.

 

1738년에 그는 오른쪽 눈에 농양을 앓고 나중에 시력이 상실되었다. 이것은 나중에 그의 삶에서 심각한 결과를 가져 오는 것이 되었다.

 

 

Berlin career(베를린에서의 경력)

 

1741년에 오일러는 과학과 철학의 ‘슈퍼 스타’ 중 한 명으로 스카웃 제의를 받고 베를린의 로얄 프러시아 과학 아카데미(Royal Prussian Academy of Sciences)에서 한 자리를 수락했다. 그곳에서의 25 년 동안, 그는 수학을 여러 주제에 적용하는 약 380 개의 기사를 썼다. 그는 또한 그가 가장 잘 알려지게 된 두 권의 책을 썼다. 하나는 1748년에 쓴 함수에 관한 교과서이자 아마도 현대 역사에서 가장 영향을 까진 수학 교과서인 “Introductio in analysin infinitorum”이며, 또 하나는 1755년에 쓴 미적분학에 관한 책 “Institutiones calculi differentialis”이다.

 

이 기간 이후 그가 쓴 세 번째 획기적인 책은 두 권으로 이루어진 “Scientia navalis”로써 두 권 다 1749년에 썼다. 이 책들은 선박의 설계를 다룬 것으로서 최대의 안정성, 조정 및 속도를 얻기 위한 것인데 실제에 있어서 이들은 서로 상대적으로 불리하게 작용하는 특징들이다.

 

 

Bernoulli’s praise(베르누이의 칭찬)

 

앞에서 언급한 요한 베르누이는 오일러보다 40살 위인데, 뉴턴이 고령으로 현업에서 퇴진을 하고 라이프니츠가 죽은 후에(1716) 의심할 여지없이 ‘Princeps Mathematicorum’(수학의 왕자)로 널리 명성을 얻었다. 그런데 그는 그가 한번 가르쳤던 학생의 훌륭함을 일찍이 알아보았다. 오일러에게 보낸 편지에서 비록 치렛말을 쓰지는 않았지만, 인사말부터 솔직한 경외심으로 급속히 상승하였다. 1745년에 그는 젊은이에게 쓰는 편지를 이렇게 시작했다: “수학자 중 왕자인 비교할 수없는 레너드 오일러에게.”(7)

 

 

Pioneering science popularization(과학의 개척을 보급화하다)

 

1759년에 오일러는 프레드릭 2세 왕의 6촌이자 프러시아의 공주로 알려지게 된 14 세의 프리드리히 샬롯 레오폴딘 루이즈(Friederike Charlotte Leopoldine Louise)의 가정교사로 요청 받았다.

 

 

(그림 5) 프리드리히 공주

 

이를 위해, 오일러는 다음 2년 동안 명료하고 적절한 평민의 용어로 그녀에게 234개의 편지를 썼지만 방정식이나 공식은 사용하지 않았다. 이 “물리와 철학에 있어서 여러 주제들에 관하여 오일러가 독일 공주에게 보냈던 편지들”은 최초에 쌍트 페텔스부르크 아카데미에서 출판되었다(1768 년에 1권과 2 권, 1772년에 3권).

 

 

(그림 6) 1768년 오일러가 독일 공주에게 프랑스어로 쓴 첫 번째 편지집

 

두 번째 프랑스어 판은 오일러가 사망한 후 1787-1789년에 파리에서 출판되었다. 이것은 볼테르의 제자인 Nicolas de Condorcet가 편집을 했는데, 그는 오일러가 하나님 및 아담과 하와에 대해 언급한 것(이는 오일러가 창세기를 역사로 믿었던 것을 보여 줌)을 예외로 두었으며, 그들 중 일부를 의도적으로 제거했다. 영어판 편집자인 Henry Hunter는 1795년 “편지들”의 영어 번역본에서 그것들 대부분을 의도적으로 복원했다.

 

칼린저는 “편지들”을 “18 세기에 작성된 가장 철저하고 권위있는 과학 대중화”라고 묘사한다.(8) 거기에 포함된 주제들로는 중력, 조수, 태양계, 뉴턴의 운동 법칙, 소리, 빛, 전기 및 자기의 성질, 대기, 열과 추위, 포탄의 궤적, 그리고 훨씬 더 많이 있다. 그는 온도계, 망원경, 및 현미경과 같은 과학 장치와 시력과 눈의 구조 등을 설명했다. 또한 그는 삼단 논법 다이어그램을 사용하여 그녀에게 논리를 가르쳤다(아래의 BOX2를 보라).

 

 

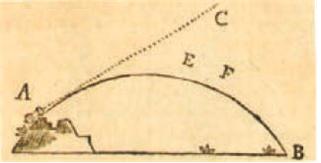
(그림 7) 포탄에 관한 중력 작용을 설명하기 위한 오일러의 그림

 

몇 통의 편지에서 오일러는 공주에게 하나님, 기도, 영원한 생명, 악과 죄, 하나님의 공의, 역경의 유용성, 죄인의 회심에 대한 자기의 생각을 전했다. “편지 41”에서 눈의 경이로움을 설명하면서 그는 다음과 같이 썼다:

 

비록 우리가 그 주제에 대해 완전한 지식에는 훨씬 미치지 못하지만, 우리가 그것에 대해 아는 아주 작은 것으로도 창조주의 능력과 지혜를 우리에게 확신시키기에 충분합니다. 우리는 눈의 구조에서 가장 뛰어난 천재라도 결코 상상할 수 없었던 완전함을 발견합니다.(9)

 

분명 세계에서 가장 학식 있는 십대인 프리드리히 공주는 편지들의 출판을 장려함으로써 그것이 널리 알려지게 했다. 1800년까지, 30판이나 나갔으며 8개의 언어로 번역되었다.

 

 

Back to St Petersburg(쌍트 페텔스부르크로 돌아가다)

 

1766년에 오일러는 쌍트 페텔스부르크에 있는 제국 아카데미(Imperial Academy)로부터의 제의를 받아들이기 위해 거기로 돌아왔다. 몇 달 후, 그는 심각한 열병에 시달렸고, 좋았던 (왼쪽) 눈에 동반된 문제가 생겨서 시력에 심각한 결함을 갖게 되었다. 칼린저는 이렇게 적고 있다:

 

거의 실명에 이르렀음에도 불구하고 그의 놀라운 기억력, 풍부한 상상력, 꾸준한 의지력, 만족을 모르는 호기심 및 학문적 직감이 계속해서 그를 잘 지원했으며, 그의 연구에 대한 중독과 가장 어려운 문제를 해결하는 즐거움이 그의 시력에 관련하여 그로 하여금 “산만한 것이 하나 더 제거되었다”고 확신있게 주장하도록 했다.(10)

 

그의 기억력이 뛰어나다는 것은 버질(Virgil)의 서사시 이니드(Aeneid/Aeneas의 유랑을 읊은 서사시)를 암송 할 수 있다는 사실에서 알 수 있으며, 이는 모든 페이지에서 어느 것이 첫 번째 줄이고 어느 것이 마지막 줄인지를 외우고 있다는 것을 나타낸다.(11)

 

누적된 시력 문제가 그의 비범한 문학적 생산성을 줄어들게 하지 않았으며, 사실상 더 증가했다! “그는 혼자서, 주 저자로써 또는 인쇄 감독하에, 415개가 넘는 일련의 기사와 서적을 관장했다. .... 이들 중 150개 이상이 그가 사망한 이후에야 출판 될 수 있었다.”(12)

 

이 기간 동안, 그는 또 다른 ‘베스트 셀러’를 만들었다: 많은 칭찬을 받는 500 페이지 분량의 “대수에 관한 완벽한 가이드(Complete Guide to Algebra)”. 1773년 4월, 그는 그의 마지막 중요한 책인 ‘간략 항법 논문’을 완성했는데, 선박의 건조 및 기동에 관한 이 완벽한 이론은 항해에 관련된 모든 사람들의 손에 보급되었다. 그 책은 해양종사자들에게 필요한 배의 이동에 관한 모든 관점을 다루었는데, 선원, 항해자, 돛대 제작자 및 선박 건조업자가 쉽게 이해할 수 있는 언어로 기록되어 있다.

 

그는 뇌졸중으로 인한 합병증으로 1783년에 사망했다.

 

 

His memory honoured(그에 대한 기억이 존경을 받다)

 

칼린저는 다음과 같이 적고 있다:

 

과학계는 위대한 동료 중의 한 명을 잃은 것으로 인식했다: 런던, 파리, 베를린, 쌍트 페텔스부르크의 4대 왕립 과학 아카데미는 오일러가 속해 있던 바젤, 리스본, 뮌헨, 스톡홀름 및 토리노의 모든 협회와 함께 이 엄청난 손실을 발표했다.(13)

 

그가 죽은 후, 쌍트 페텔스부르크 아카데미는 출판되지 않은 그의 저작물을 가지고 있었는데 그것은 거의 50여 년 동안 계속 발행하기에 충분한 양이었다. 1911년 이래로 스위스 과학 아카데미 (Swiss Academy of Sciences)는 오일러의 “Opera Omnia//오페라 옴니아”(수집된 작품)를 출판해 오고 있다. 지금(2017)까지, 약 72권의 4절판 책이 인쇄되었는데, 그것은 수학, 천문학을 포함한 역학, 그리고 잡학의 세 개의 시리즈로 되어 있으며, 대략 35,000 페이지에 이른다. 네 번째 시리즈는 10권의 책으로 구성되며, 거기에는 현존하는 오일러의 3,300개의 편지와 프랑스어, 라틴어, 독일어, 러시아어 및 (약간의) 영어로 쓴 275 개의 답신이 들어가는데 현재 제작 중이다.

 

 

(그림 8) 바젤 대학교 창립 500 주년을 기념하기 위해 1960년에 리엔(Riehen)에서 제막된 오일러 명판. 그의 이름과 년도 아래의 텍스트에 이렇게 적혀있다: 수학자, 물리학자, 엔지니어, 천문학자 그리고 철학자. Riehen에서 젊은 시절을 보냈다. 그는 위대한 학자이자 친절한 사람이었다.

 

 

그는 수많은 스위스, 러시아, 독일 및 기타 국가의 우표와 스위스 10 프랑 지폐에 등장했다. 그리고 오일러를 기리기 위해, 천문학자들은 달의 분화구와 소행성을 그의 이름으로 명명했다.

 

점잖고 겸손했던 그는 그 시대의 가장 위대한 수학자였다. 그가 생을 마칠 때까지 유럽의 모든 수학자들은 그를 그들의 선생으로 여겼으며, 이는 19세기와 20세기까지 그러했다. 예를 들어, 저명한 프랑스 수학자(그리고 무신론자)인 Pierre Simon Laplace(1749-1827)는 이렇게 말했다: “오일러를 읽어라. 오일러를 읽어라; 그는 우리 모두의 주인이시다!”(14) 그리고 오일러는 전적으로 헌신적이며 하나님을 경외하고 성경을 믿는 기독교인이었다.

 

 

References and notes(참고문헌과 각주)

 

1. See Ronald S. Calinger’s monumental biography, Leonard Euler: Mathematical Genius in the Enlightenment, Princeton University Press, USA, 2016, a major source for this article.

2. Fellmann, Emil A., Leonard Euler (in German), Rowohlt Taschenbuch Verlag, Reinbek bei Hamburg, Germany, P. 9. Fellmann(1927-) whose academic background is in mathematics, physics and philosophy, has been a visiting professor/lecturer at a number of European universities, including the University of Bonn.

3. Calinger, Ref. 1, p. 11.

4. Calinger, Ref. 1, p. 92.

5. Calinger, Ref. 1, p. 188.

6. He later published a more rigorous proof, and contributions from other mathematicians are also available in his reference.

7. Fellmann, ref. 2, p. 24.

8. Calinger, Ref. 1, p. 465.

9. Letters of Euler to a German Princess, trans. by Henry Hunter, Vol. 1, No. 41, p. 165, 1802.

10. Calinger, Ref. 1, p. 454.

11. The Aeneid is a Latin epic poem, written by Virgil between 29 and 19 BC, that comprises 9,896 lines in dactylic hexameter.

12. Calinger, Ref. 1, p. 456.

13. Calinger, Ref. 1, p. 532.

14. Journal des Savants, January 1846, p. 51.

 

 

RUSSELL GRIGG, M.Sc(Hons.)

was an industrial chemist before serving 20 years with Overseas Missionary Fellowship (now OMF International). He is a staff member of Creation Ministries International in Australia. For more: creation.com/grigg.

 

 

BOX1: EULER VS BIBLE SKEPTICS(오일러 대 성경 회의론자)

 

오일러는 ‘계몽주의’라고 잘못 이름 붙여진 시대에 살았다. 그때는 Voltaire(1694-1778), Hume(1711-1776), Kant(1724-1804) 등과 같은 회의주의 철학자들과 그들의 동료인 ‘자유사상가’들이 성경적 개념의 하나님을 조롱하고, 기독교 신앙을 부인하고, 오직 이성의 변화를 통해서만 인간성이 개선될 수 있다고 선언했다. 이 모든 것을 통해서, 오일러는 확고하게 자신의 기독교 신앙을 유지했으며, 1746년에는 그 당시의 회의론에 대한 열렬한 반응으로 “자유사상가들의 반대에 대항하는 요한계시록(즉, 성경)에 대한 반론”이라는 제목의 책을 썼다. 이것은 53 개의 번호가 붙은 단락으로 구성된 팜플렛이다.

 

그는 하나님이 진리이시고 세상은 그분의 전능하심과 지혜의 산물이므로 행복은 진리를 이해하는 것을 포함한다고 주장함으로써 이 책을 시작했다. 계속해서 그는 하나님이 모든 진리의 원천이며 궁극적인 선이라고 말한다. 하나님은 인간의 마음 속에 자연 법칙을 기록 하셨고 그것은 인간의 행동이 이 법을 준수할 것을 요구한다. 또한 이 법은 하나님 자신으로부터 유래된 것이므로, 이에 불순종 하는 것은 전능하신 하나님을 거역하는 반역이며, 이것은 하나님의 심판을 가져온다.

 

오일러는 우리의 모든 의무의 유일하고도 진정한 원천을 성경이 제시한다고 주장했는데, 그것은 각 저자의 재능에 기인할 수 없는 방식으로 되어 있으므로 성경이 하나님으로부터 온 것으로 간주한다고 한다. 수많은 신자들이 그리스도께서 죽음으로부터 살아나신 후에 그분을 보았을 뿐 아니라 그분과 대화를 나누었으므로, 이것은 그들의 상상의 산물이 아니었다. 그러므로 예수 그리스도의 부활은 의심할 여지가 없는 사실이며, 전적으로 하나님이 하신 일이므로, 따라서 우리는 이 생애와 앞으로 올 세상 모두에 대한 복음의 모든 약속을 믿을 수 있다.

 

자유사상가에 관련하여 오일러는 성경의 신성이 단호하게 주장하는 논점들에 대해서는 그들이 어떤 반박도 제시할 수 없다고 말했다. 그렇다. 성경은 자유사상가들이 동의하지 않는 것을 포함하고 있다. 그렇지 않다면 이것은 성경에 해로울 것이다. 성경에 들어있는 명백한 모순과 관련하여 수학을 포함하여 어떤 과학도 유사하거나 더 강한 비판으로도 재반박을 할 수는 없다. 그런데 아무도 수학의 확실성을 기각하지 못한다. 자유사상가들의 반대는 오랫동안 철저히 논박되어 왔지만, 그들은 진실에 대한 열망에서 기인하지 않았기 때문에 논박을 거부하고 빈약하고 불합리한 반대를 계속적으로 반복한다고 오일러는 말했다.

 

 

BOX2: EULER DIAGRAMS THAT TEACH LOGIC(논리를 가르치는 오일러 도표)

 

일반적으로 오일러에 기인한 덜 알려져 있는 발명 중 하나는 프리드리히(Friederike) 공주에게 논리를 가르치기 위해 사용한 삼단 논법 다이어그램이다. 그는 이것을 편지 103, 398쪽에서 처음 사용하였고, 그 이후 편지 108을 포함하여 거기까지 다양한 가상 상황에 그것을 적용하였다. 1960 년 이래 오일러 다이어그램(지금은 사람들이 이렇게 부른다)은 벤다이어그램(1880년경 존 벤이 오일러 다이어그램이 중첩되는 특별한 경우)과 함께 집합의 서로 다른 원소들의 관계를 설명하는 데에 사용해오고 있다. 중요한 것은 곡선의 크기나 모양이 아니라 그것들이 어떻게 중첩되는가 하는 것이다. 다른 곡선 안에 완전히 포함되는 곡선은 그것의 부분집합을 나타낸다.

 

 

(그림 9)프리드리히 공주에게 보낸 그의 편지 103에 있는 오일러 도표. 그는 그녀에게 논리를 가르치기 위해 이 도표를 사용했다.

 

 

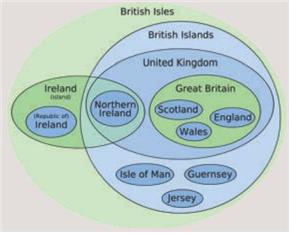
(그림 10) 영국제도에 관한 오일러 도표(위키피디아)

 

 

BOX3: EULER’S INFLUENCE IN TODAY’S MATHEMATICS(오늘날 수학에 있어서 오일러의 영향)

 

오늘날 사용되는 많은 수학 용어와 표기법은 오일러에 의해 작성되고, 대중화되거나 표준화되었다. 거기에는 다음과 같은 것들이 포함된다:

 

* 함수를 나타내는 f(x)

* 미지수에 사용하는 x, y, 그리고 z

* 삼각형의 변에 사용하는 a, b, c

* 대각에 사용하는 A, B, C

* 삼각형의 외접원 반경과 내접원 반경에 사용하는 R과 r

* 삼각함수의 축약형 sin, cos, tan, csc, sec, cot

* π의 광범위한 사용(그가 이 표기를 처음 사용한 것은 아니다)

* 합계에 사용하는 Σ

* 유한 차분에 사용하는 Δ

* 허수 √-1에 사용하는 i

* e=2.71828인 자연로그에 사용하는 밑 e

* 기둥의 임계하중에 관한 오일러 공식: P_cr = π²EI/(KL)²

* 오일러에서 기인하며 오일러 정체성(Euler identity)이라 불리는 공식 eiπ = -1(eiπ + 1 = 0로 현대화 되었다). 수학자들은 이것이 모든 수학 공식 중 가장 아름다운 공식이라고 칭송한다. 왜냐하면 이 공식은 매우 많은 것을 말하기 때문이다. 즉, 가장 중요한 다섯 개의 수학 상수가 하나의 공식에 모두 나타난다.

* 오일러의 다면체 공식 또한 오일러 특유의 것이라고 알려져 있다: V – E + F =2(여기서 V=꼭지점의 수, E=면의 수, 그리고 F=단순한(즉, 구멍이 없는) 3차원 볼록 다면체의 면의 수).

 

더 많은 것은 다음을 참고하라. en.wikipedia.org/wiki/List_of_things_named_after_Leonhard_Euler